Program: Measurement and Control for
Quantum Computing



Researchers in the Centre for Quantum Computer Technology (and
related researchers) at Griffith University in
2003.
From left to right, David Pegg (Professor), Jay
Gambetta
(Ph.D.), Howard Wiseman (Assoc. Professor, Program Manager), Damian Pope
(post-doc; not a member),
Kurt Jacobs
(post-doc), Josh
Combes
(Honours), Laura Thomsen (Ph.D), Daniel Atkins (Ph.D.), Neil Oxtoby
(Ph.D),
Kenny Pregnell (Ph.D.), and Josh Garretson (Honours; not a member).
The Centre for Quantum Computer
Technology
was established as an Australian Research Council Centres of Excellence
in 2003. It has research programs at six Australian Universities: New
South Wales, Melbourne, Queensland,
Macquarie,
Griffith, and Sydney. Its primary aim is to build a
prototype Silicon-based quantum computer (to be done at the University
of New South Wales), but there are several other research directions,
experimental
and theoretical. The Griffith Program is Measurement and Control for Quantum
Computing. It supports wide-ranging theoretical research in
quantum measurement, control and information. For more
information on the program, see below, or see the Program Page (under construction) on
the CQCT website.
The Griffith Program: Measurement and Control for Quantum Computing.
1. Quantum Measurement Theory for Read-Out Devices
A crucial part of quantum computing is read-out. Schemes for reading
out
the state of a solid-state QC include a single-electron transistor, a
quantum
point contact, and a micromechanical cantilever. We plan both to
develop
more sophisticated theories for such schemes, and to investigate other
schemes. The theory of quantum trajectories, as developed in quantum
optics,
has proven very useful for understanding continuous measurement in the
solid state context. However, as traditionally formulated it is a
highly
idealized theory, assuming that individual quantum events (such as
electrons
tunnelling through a barrier) can be observed. In practice, the
electronic
noise and impedance of the external circuit will mask this. A
generalization
of the quantum trajectory approach to describe the effect of such
read-out
imperfections on the conditioned system state has recently been
developed
for photon detectors (Warszawski, Wiseman and Mabuchi, 2002). This
technique
is now being applied in the solid-state context.
2. Quantum Feedback Control
Applications for quantum feedback in quantum computers include quantum
error correction for detected errors, testing read-out devices, state
engineering,
and measurement engineering. State engineering requires a general
understanding
of quantum control, which will be sought. Measurement engineering by
feedback
means adaptive measurements, which
could be useful in linear optics quantum computing.
3. Quantum Information - Measurement Interface
Dissipation is the transfer of energy from the system to the
environment.
It is now well understood that what is more relevant for quantum
computers
is decoherence, the transfer of information from the system to the
environment.
This information is quantum information, but it can be turned into
classical
information by measuring the environment. This new perspective on
quantum
measurement theory is a fruitful field for investigation.
4. Quantum Computing - Measurement Interface
This part of the program will seek new schemes for quantum measurement
as they may be useful for quantum computing. On the flip-side, quantum
algorithms should also suggest new measurement schemes.
2003 Annual Report on the Research Program Measurement and Control
in Quantum Computing.
Program Manager
A/Prof Howard Wiseman, GU
Measurement and Control Researchers
Students: Mr Neil Oxtoby (PhD), Mr
Kenneth Pregnell (PhD), Ms Laura Thomsen (PhD), Mr Daniel Atkins (PhD),
Mr Joshua Combes (Honours)
Staff: Prof David Pegg, Dr Kurt
Jacobs, Mr Jay Gambetta, Dr He-Bi Sun (UQ)
Collaborating Centre Researchers
University of Queensland: Prof
Gerard Milburn, A/Prof Tim Ralph
Other Collaborators
Macquarie University / University of
Queensland: Dr Stephen Bartlett
University of Hertfordshire: Dr John
Vaccaro
California Institute of Technology:
A/Prof Hideo Mabuchi, Ms Charlene Ahn, Mr Asa Hopkins
Los Alamos National Laboratory: Dr
Salman Habib, Dr Tanmoy Bhattacharya, Dr Daniel Steck
University of Maryland: Dr Keith
Schwab
Program Description
The aim of this program is to
understand the measurement and control of devices operating on a
quantum scale and to apply this understanding to quantum information
processing. The program has four sub-programs: Quantum Measurement
Theory for Read-Out Devices; Quantum Feedback Control; Quantum
Information -- Measurement Interface; Quantum Computing -- Measurement
Interface.
1.
Quantum Measurement Theory for Read-Out Devices
 The aim of this sub-program is
to develop methods for determining the state of a qubit (or register)
conditioned on the results of monitoring the qubit using a realistic
read-out device. That is, for example, the measurement record is
filtered and has noise added by the external circuit containing the
detector that couples to the qubit [Oxtoby et al, J. Phys. C 15,
8055-64 (2003)]. The main outcome for this year [Oxtoby et al,
submitted] is that we have formulated a rigorous method for deriving a
quantum trajectory (that is, the stochastic evolution for the
conditioned system state) for a large class of solid-state detectors in
a simplified external circuit, as shown in Figure 1. We have also
investigated realistic detection in a cavity QED context, to see its
effect on estimating an unknown parameter (the position of the atom)
from the detection record [Warszawski et
al, submitted]. This is
relevant for quantum computing in that domain.
The aim of this sub-program is
to develop methods for determining the state of a qubit (or register)
conditioned on the results of monitoring the qubit using a realistic
read-out device. That is, for example, the measurement record is
filtered and has noise added by the external circuit containing the
detector that couples to the qubit [Oxtoby et al, J. Phys. C 15,
8055-64 (2003)]. The main outcome for this year [Oxtoby et al,
submitted] is that we have formulated a rigorous method for deriving a
quantum trajectory (that is, the stochastic evolution for the
conditioned system state) for a large class of solid-state detectors in
a simplified external circuit, as shown in Figure 1. We have also
investigated realistic detection in a cavity QED context, to see its
effect on estimating an unknown parameter (the position of the atom)
from the detection record [Warszawski et
al, submitted]. This is
relevant for quantum computing in that domain.
Figure
1. Circuit diagram for a "realistic" read-out device. The
read-out on which the state of the CQD
(coupled quantum dots) qubit is conditioned is the current through the
Ammeter A. This represents the output of a Current Amplifier which adds
noise as it amplifies. The bias voltage also contains noise. The
Detector could be a DC SET (Single Electron Transistor) or a QPC
(Quantum Point Contact).
2.
Quantum Feedback Control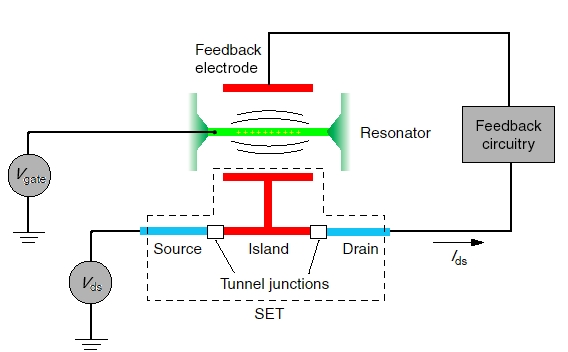
The aim of this sub-program is
to investigate feedback control of quantum systems useful for quantum
information processing, such as error correction of quantum registers,
or cooling a system down to its lowest two quantum states. This year we
have published a paper establishing a protocol to protect a quantum
register against detected errors using only a single additional qubit
[Ahn et al, Physical Review A
67, 052310 (2003)]. Work is
underway to
generalize this for more than one type of detected error per
qubit. In
addition, we have considered motional cooling to close to the ground
state in both a cavity QED system [Steck et al, submitted] and a
nanomechanical system (see Figure 2) [Hopkins et al, SPIE 5276 (2003)].
Figure
2. Diagram for the
cooling of a nanomechanical resonator close to its ground state using
feedback based on continuous monitoring by an SET. This device is
currently being built at the Laboratory for Physical Sciences,
University of Maryland.
3.
Quantum Information -- Measurement Interface
 The aim of this sub-program is to study
questions at the interface of quantum information and quantum
measurement. The main outcome for this year has been (i) to generalize
the concept of super-selection rules (SSRs) to describe a large class
of restrictions on measurements and other quantum operations and (ii)
to calculate the entanglement two parties can distill from a state they
share, given a restriction in this class. This work [Wiseman and
Vaccaro, Physical Review Letters 91,
097902 (2003); Bartlett and Wiseman, Physical Review Letters 91, 097903 (2003)] is significant
for quantum information processing (QIP) in systems subject to SSRs,
such as Bose-Einstein condensation, or NMR ensemble quantum
computing. Another outcome has been to derive fundamental
inequalities relating to information extraction and the purification of
conditioned states in measurements on a quantum system drawn randomly
from an ensemble [Jacobs, Physical Review A 68, 054302 (2003)]. Thirdly, we have
examined the question of the validity of optical continuous variable
quantum teleportation, and concluded that a laser should be regarded as
a clock, not a quantum channel [Wiseman, J. Opt. B (to be published)].
Finally, we have investigated the preparation of spin-squeezed states
for the purposes of interferometric measurement of phase shifts [Combes et al, unpublished]. We find that
the maximally spin squeezed state (shown in Figure 3) is not the
optimal state for this purpose, and we identify a simple scheme to
produce the optimal state.
The aim of this sub-program is to study
questions at the interface of quantum information and quantum
measurement. The main outcome for this year has been (i) to generalize
the concept of super-selection rules (SSRs) to describe a large class
of restrictions on measurements and other quantum operations and (ii)
to calculate the entanglement two parties can distill from a state they
share, given a restriction in this class. This work [Wiseman and
Vaccaro, Physical Review Letters 91,
097902 (2003); Bartlett and Wiseman, Physical Review Letters 91, 097903 (2003)] is significant
for quantum information processing (QIP) in systems subject to SSRs,
such as Bose-Einstein condensation, or NMR ensemble quantum
computing. Another outcome has been to derive fundamental
inequalities relating to information extraction and the purification of
conditioned states in measurements on a quantum system drawn randomly
from an ensemble [Jacobs, Physical Review A 68, 054302 (2003)]. Thirdly, we have
examined the question of the validity of optical continuous variable
quantum teleportation, and concluded that a laser should be regarded as
a clock, not a quantum channel [Wiseman, J. Opt. B (to be published)].
Finally, we have investigated the preparation of spin-squeezed states
for the purposes of interferometric measurement of phase shifts [Combes et al, unpublished]. We find that
the maximally spin squeezed state (shown in Figure 3) is not the
optimal state for this purpose, and we identify a simple scheme to
produce the optimal state.
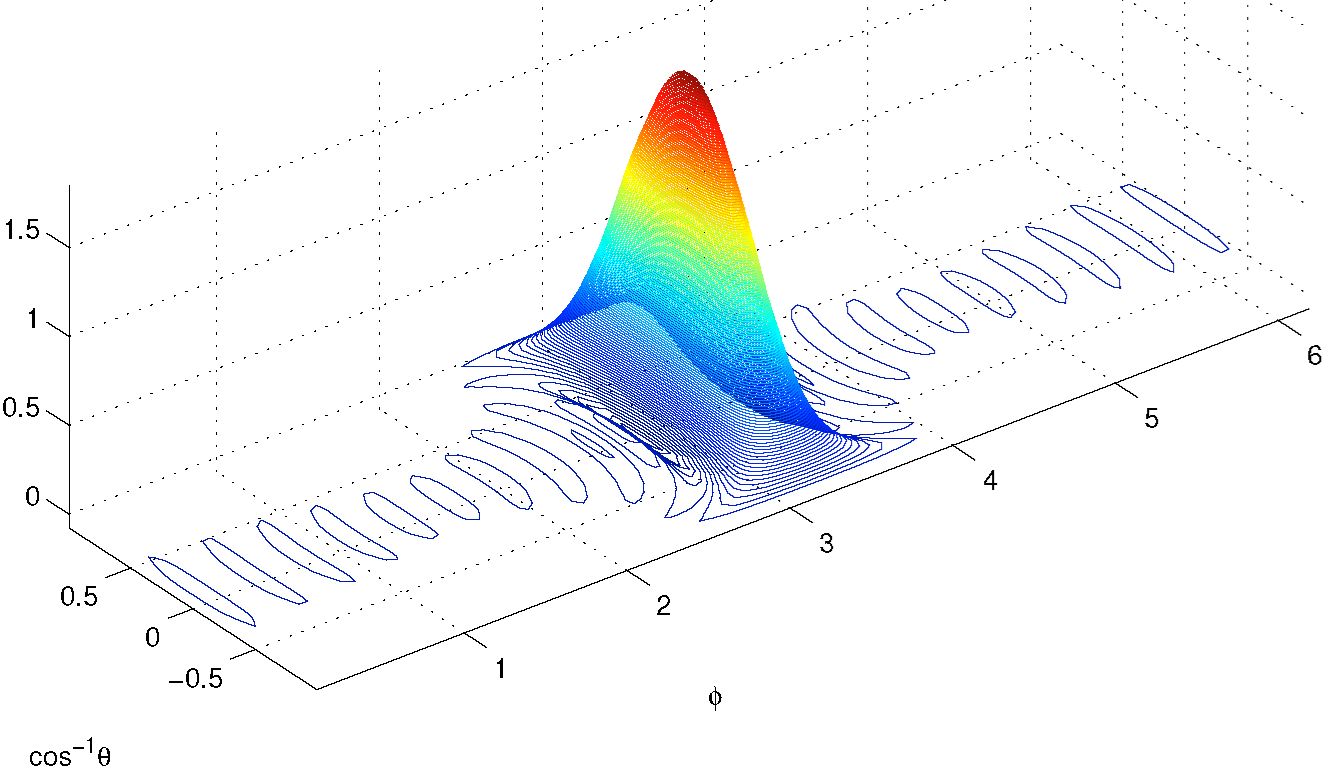
Figure
3. Wigner function for the
maximally spin squeezed state of an ensemble of 20 atoms, plotted as a
function of polar co-ordinates for the spin direction. Note the
"ripples" (positive and negative fluctuations) in the tails of the
distribution. These make this state sub-optimal for single-shot
measurement of the shift in the phase f (which could be produced by a
magnetic field, for example)
4.
Quantum Information -- Computing Interface
The aim of this sub-program is
to study
questions at the interface of quantum information and quantum
computing. The main outcome for this year has been the discovery of a
general scheme to retrodict quantum states in optics using only
coherent states and beam splitters [Pregnell and Pegg, J. Mod. Opt. (to
be published)]. That is, it is possible to engineer an optical device
such that one particular measurement result corresponds to a given
(arbitrary) element in a positive operator measure (POM). We have
also discovered a simpler scheme for the specific problem where the POM
is that arising from measurement of the Pegg-Barnett phase operator
[Pregnell and Pegg, Physical Review A 67, 063814 (2003)]. This scheme
(shown in Figure 4) requires a binomial input state as a reference
field, but we show that this can be approximated by a squeezed state
for low photon numbers.
Figure
4. Eight-port
interferometer for measuring the canonical phase distribution of weak
fields. The field to be measured is in the input port labeled In 0, the
reference field in state is in input port In 1, and vacuum state fields
are in In 2 and In 3. A photodetector is in each output port. The
rectangles are phase shifters.
Return to
Howard Wiseman's Home Page





 The aim of this sub-program is
to develop methods for determining the state of a qubit (or register)
conditioned on the results of monitoring the qubit using a realistic
read-out device. That is, for example, the measurement record is
filtered and has noise added by the external circuit containing the
detector that couples to the qubit [Oxtoby et al, J. Phys. C 15,
8055-64 (2003)]. The main outcome for this year [Oxtoby et al,
submitted] is that we have formulated a rigorous method for deriving a
quantum trajectory (that is, the stochastic evolution for the
conditioned system state) for a large class of solid-state detectors in
a simplified external circuit, as shown in Figure 1. We have also
investigated realistic detection in a cavity QED context, to see its
effect on estimating an unknown parameter (the position of the atom)
from the detection record [Warszawski et
al, submitted]. This is
relevant for quantum computing in that domain.
The aim of this sub-program is
to develop methods for determining the state of a qubit (or register)
conditioned on the results of monitoring the qubit using a realistic
read-out device. That is, for example, the measurement record is
filtered and has noise added by the external circuit containing the
detector that couples to the qubit [Oxtoby et al, J. Phys. C 15,
8055-64 (2003)]. The main outcome for this year [Oxtoby et al,
submitted] is that we have formulated a rigorous method for deriving a
quantum trajectory (that is, the stochastic evolution for the
conditioned system state) for a large class of solid-state detectors in
a simplified external circuit, as shown in Figure 1. We have also
investigated realistic detection in a cavity QED context, to see its
effect on estimating an unknown parameter (the position of the atom)
from the detection record [Warszawski et
al, submitted]. This is
relevant for quantum computing in that domain.
 The aim of this sub-program is to study
questions at the interface of quantum information and quantum
measurement. The main outcome for this year has been (i) to generalize
the concept of super-selection rules (SSRs) to describe a large class
of restrictions on measurements and other quantum operations and (ii)
to calculate the entanglement two parties can distill from a state they
share, given a restriction in this class. This work [Wiseman and
Vaccaro, Physical Review Letters 91,
097902 (2003); Bartlett and Wiseman, Physical Review Letters 91, 097903 (2003)] is significant
for quantum information processing (QIP) in systems subject to SSRs,
such as Bose-Einstein condensation, or NMR ensemble quantum
computing. Another outcome has been to derive fundamental
inequalities relating to information extraction and the purification of
conditioned states in measurements on a quantum system drawn randomly
from an ensemble [Jacobs, Physical Review A 68, 054302 (2003)]. Thirdly, we have
examined the question of the validity of optical continuous variable
quantum teleportation, and concluded that a laser should be regarded as
a clock, not a quantum channel [Wiseman, J. Opt. B (to be published)].
Finally, we have investigated the preparation of spin-squeezed states
for the purposes of interferometric measurement of phase shifts [Combes et al, unpublished]. We find that
the maximally spin squeezed state (shown in Figure 3) is not the
optimal state for this purpose, and we identify a simple scheme to
produce the optimal state.
The aim of this sub-program is to study
questions at the interface of quantum information and quantum
measurement. The main outcome for this year has been (i) to generalize
the concept of super-selection rules (SSRs) to describe a large class
of restrictions on measurements and other quantum operations and (ii)
to calculate the entanglement two parties can distill from a state they
share, given a restriction in this class. This work [Wiseman and
Vaccaro, Physical Review Letters 91,
097902 (2003); Bartlett and Wiseman, Physical Review Letters 91, 097903 (2003)] is significant
for quantum information processing (QIP) in systems subject to SSRs,
such as Bose-Einstein condensation, or NMR ensemble quantum
computing. Another outcome has been to derive fundamental
inequalities relating to information extraction and the purification of
conditioned states in measurements on a quantum system drawn randomly
from an ensemble [Jacobs, Physical Review A 68, 054302 (2003)]. Thirdly, we have
examined the question of the validity of optical continuous variable
quantum teleportation, and concluded that a laser should be regarded as
a clock, not a quantum channel [Wiseman, J. Opt. B (to be published)].
Finally, we have investigated the preparation of spin-squeezed states
for the purposes of interferometric measurement of phase shifts [Combes et al, unpublished]. We find that
the maximally spin squeezed state (shown in Figure 3) is not the
optimal state for this purpose, and we identify a simple scheme to
produce the optimal state.